[Home]

Table of contents

আরো কিছু আলোচনা

আরো কিছু আলোচনা

L'Hopital's rule

এই জিনিসটা আমার বইতে রাখি নি, কারণ এটা না বুঝে লাগিয়ে বসলে অনেক সময়ে একটা বিচ্ছিরি ব্যাপার হয়--ভুল পদ্ধতিতে ঠিক উত্তর এসে যায়! পরীক্ষার খাতায় এরকম ব্যাপার হলে মাস্টারমশাইরা নম্বর কাটেন, এবং ছাত্ররা অবাক হয়ে ভাবে--উত্তর তো ঠিকই হয়েছিল, তবে নম্বর কাটা গেল কেন? তবে আজকাল যেরকম MCQ-এর হিড়িক, সেখানে উত্তর আন্দাজ করতে পারলেই নম্বর, ঠিক বেঠিক সব কায়দাই সমান৷ তাই এখানে এই কায়দাটার একটু আলোচনা করি৷ ব্যাপারটা এই--
ধরো $f(x)$ আর $g(x)$ দুটো function. তোমাকে বার করতে দিয়েছে $$\lim_{x\rightarrow a}\frac{f(x)}{g(x)}.$$ এদিকে $\lim_{x\rightarrow a}f(x)$ আর $\lim_{x\rightarrow a}g(x)$ দুজনেই $0.$ মানে যে limit-টা বার করতে দিয়েছে, সেটা $\frac00$ জাতীয় হয়ে যাচ্ছে৷ তখন $f(x)$ আর $g(x)$-এর জায়গায় ওদের derivative বসিয়ে দ্যাখো $$\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}$$ কী হয়৷ যদি এটা বার করতে পারো, তো আমাদের গোড়ার limit-টাও সেটাই হবে! যদি দ্যাখো এটাও $\frac00$ চেহারার হয়ে যাচ্ছে, তবে আরেকবার differentiate করে $$\lim_{x\rightarrow a}\frac{f''(x)}{g''(x)}$$ বার করার চেষ্টা করে দ্যাখো৷
ব্যাপারটা বেশ ম্যাজিকের মত৷ অবশ্য এটা কাজ করার জন্য $f(x)$ আর $g(x)$-কে differentiable হতে হবে৷ আর গোড়ার limit-টার চেহারা হতে হবে $\frac00$-এর মত (আসলে $\frac\infty\infty$ হলেও চলবে)৷ আরেকটা সুক্ষ্ম শর্তও আছে৷ $a$-কে ঘিরে খানিক দূর পর্যন্ত যেন $g'(x)$-টা $\neq 0$ হয়৷ ঠিক $a$-তে যদি $g'(x)=0$ হয়ে যায়, তাতে আপত্তি নেই৷ যেমন যদি $(a-1,a)$ আর $(a,a+1)$-এর উপরে $g'(x)\neq 0$ হয়, তবেই আমরা খুশি৷ এই কায়দাটা বার করেছিলেন Bernoulli নামের একজন গণিতজ্ঞ৷ এটা যখন তিনি বার করেন, তখন তিনি এক জমিদারকে অংক শেখাতেন এই শর্তে যে, সেই সময়ের মধ্যে যা যা Bernoulli আবিষ্কার করবেন, সব কিছুই সেই জমিদার মশায় নিজের নামে একটা বই করে ছাপাবেন৷ জমিদারমশায়ের নাম ছিল L'Hopital. সেই থেকেই কায়দাটার নাম হয়েছে L'Hopital's rule. শুনেছি নিজের আবিষ্কারের উপর জমিদারমশায়ের নামের লেবেল দেখে Bernoulli বড়ই দুঃখ পেয়েছিলেন৷

যাই হোক, এবার একটা ছোট্টো প্রয়োগ দেখাই--

ধরো বার করতে বললাম $$\lim_{x\rightarrow 0}\frac{1-\frac{x^2}{2}-\cos x}{x^4}.$$ এটা একটা $\frac00$ চেহারার limit. সহজে করা যাচ্ছে না৷ উপর নীচকে differentiate করে দাও, পাবে $$\lim_{x\rightarrow 0}\frac{x+\sin x}{4x^3}.$$ এতেও সুবিধা হচ্ছে না৷ Limit-টা এখনও $\frac00$ চেহারাতেই রয়ে গেছে৷ আবার differentiate করো-- $$\lim_{x\rightarrow 0}\frac{1+\cos x}{12x^2}.$$ ধ্যাত্তেরি, এখনও $\frac00$ চেহারা তো গেল না৷ আবার differentiate করো-- $$\lim_{x\rightarrow 0}\frac{-\sin x}{24x}.$$ এইবার দেখা যাচ্ছে যে, উত্তর হবে $-\frac{1}{24}.$ সুতরাং আমাদের গোড়ার limit-টাও এটাই হবে৷

তবে আমার বইতে আমি infinite series ব্যবহার করে যে কায়দা আলোচনা করেছি, সেটা দিয়েই এইরকম অংক বেশী সহজে হয়৷

এবার বলি অন্ধের মত L'Hopital's rule লাগাতে গিয়ে কোথায় ভুল হতে পারে৷ ধরো বলল $$\lim_{x\rightarrow 0}\frac{\sin x}{x}$$ বার করতে৷ এটাও $\frac00$ চেহারার৷ তাই L'Hopital's rule লাগলে পাবে $$\lim_{x\rightarrow 0}\frac{\cos x}{1}=1.$$ এটা অবশ্যই ঠিক উত্তর৷ কিন্তু অনেক মাষ্টারমাশাই এতে চটে যাবেন৷ তাঁদের বক্তব্য হল--
এই যে বাপু $\sin x$-কে differentiate করে $\cos x$ লিখে দিলে সেটা কী করে পেয়েছিলে? নিশ্চয়ই এইভাবে-- $$\frac{d\sin x}{dx} = \lim_{h\rightarrow0}\frac{\sin (x+h)-\sin x}{h} = \lim_{h\rightarrow0}\frac{2\sin \frac{h}{2}\cos x}{h}.$$ এবার $t=\frac{h}{2}$ বসালে এটা হয়ে যায় $$ = \cos x\lim_{t\rightarrow0}\frac{\sin t}{t} = \cos x.$$ এখানেই তো তুমি ভিতরে ভিতরে $\lim_{t\rightarrow0}\frac{\sin t}{t}=1$ ব্যবহার করলে, ঠিক যেটা তোমার প্রমাণ করার কথা ছিল!
অবশ্য $\frac{d\sin x}{dx}$ যে $\cos x$ হয়, এটা অন্য পথেও প্রমাণ করা যায়, এবং সেই পথে এগোলে L'Hopital's rule প্রয়োগে কোনো বাধা নেই৷ কিন্তু এতসব গোলমাল এড়াবার জন্য আমি বই থেকে L'Hopital's rule-এর আলোচনা বাদ রেখেছিলাম৷

Composition

দুটো function-এর composition কী জিনিস সেটা বইটায় অনেক আলোচনা করেছি৷ যদি দুটো function-কেই একাধিক ফর্মুলায় ভেঙে দেওয়া থাকে, তবে তাদের composition বার করতে অনেকের অসুবিধা হয়৷ নীচের অংকটা সেরকম একটা উদাহরণ৷ এটা IIT-র পরীক্ষায় এসেছিল, 1983-তে৷ বলা আছে $f(x)=\left\{\begin{array}{ll}1+x&\text{if }0\leq x\leq 2\\ 3-x&\text{if }2< x\leq 3\\\end{array}\right..$ এ থেকে তোমাকে $f(f(x))$ বার করতে হবে, এবং সেটা কোথায় কোথায় continuous নয় বলতে হবে৷

উত্তরটা ধাপে ধাপে করে দেখাই৷

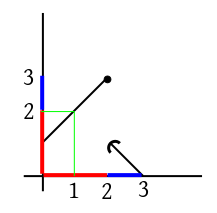
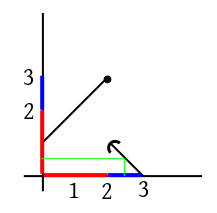
প্রথমে $f(x)$-এর গ্রাফ এঁকে নাও
বিভিন্ন ফর্মুলার জায়গাগুলো আলাদা আলাদা রঙে দাগ দিয়ে নিলাম৷ $x$-axis-এ ভিতরের function-টার জন্য, আর $y$-axis-এ বাইরের function-টার জন্য৷ এখানে অবশ্য বাইরে ভিতরে দু জায়গাতেই $f(x)$ আছে৷
এবার মনে মনে কোনো একটা $x$ নিয়ে তার জন্য সবুজ লাইনটার মত একটা লাইন টানো৷ মনে মনে $x$-টাকে বাঁদিক থেকে ডানদিকে সরাতে থাকো৷ এখানে সবুজ লাইনটা লাল থেকে শুরু হয়ে লালে শেষ, তার মানে $1+x$-এর পেটে $1+x$ ঢুকবে, মানে $1+(1+x) = 2+x.$
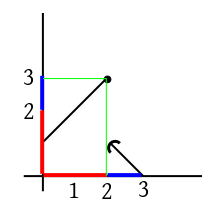
এই $2+x$-এর মেয়াদ চলবে এতটা অবধি৷ এবার থেকে সবুজ লাইনটা ক্ষ লালে শুরু, নীলে শেষ৷ মানে $3-x$-এর পেটে $1+x$ ঢুকবে, $3-(1+x) = 2-x.$
এই $2-x$ চলবে এতটা পর্যন্ত৷ এরপর থেকে নীলে শুরু, লালে শেষ, মানে...
... $1+x$-এর পেটে $3-x$ ঢুকবে, ফলে হবে $1+(3-x) = 4-x.$
সুতরাং সব মিলিয়ে দাঁড়ালো $$f(f(x))=\left\{\begin{array}{ll} 2+x &\text{if }0\leq x \leq 1\\ 2-x &\text{if }1< x \leq 2\\ 4-x &\text{if }2\leq x \leq 3\\ \end{array}\right.$$ এর discontinuity খালি দু জায়গায় $1$ আর $2$-তে৷

বিভিন্ন প্রচলিত function-দের ধর্মাবলী

বইটায় নানারকম function-এর আলোচনা করেছি৷ প্রসঙ্গক্রমে তাদের বিভিন্ন ধর্মেরও উল্লেখ করা হয়েছে৷ তাতে করে ধর্মগুলো সারা বইতে ছড়িয়ে ছিটিয়ে গেছে, আবার কিছু কিছু দরকারী জিনিস বাদ পড়ে গেছে৷ সেগুলোকে একত্র করার চেষ্টা করা যাক৷

$y=c,$ যেখানে $c$ কোনো constant

$y=x,$ যার আরেক নাম identity function

$y=x^2$

$y=|x|$

$y=|x|$

$y=[x]$

$y=x-[x],$ যাকে অনেক সময়ে $\{x\}$ লেখে (fractional part of $x$)

$y=\sin x$

$y=\cos x$

$y=\tan x$

$y=e^x$

$y=\log x$