Learning J

First taste of J

Now let us look at a simple example in the light of what we have learnt so far. In this example we shall give a taste of all the features we have talked about so far. We start with an array of numbers 1,3,4,5,10. J will consider this as a tree of depth 1.

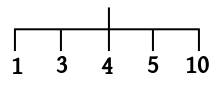
x=: 1 3 4 5 10

To find the number of highest level branches J provides a monad called #. Let's put it to use:

# x

J responds with 5. Notice how I described # in terms of the input tree, and not as "a function to find the length of a list".

Next, we shall see the arithmetic operations in J. The operations for addition, subtraction and multiplication are usual. But J uses % for division. All operations are done using floating points (more on this later).

The expression

3 * 4 - 10 % 5

is interpreted as $$ 3\times (4 - (10 \div 5)). $$ Amuse yourself by trying to guess the result of

5 - 1 - 1 - 1 - 1 - 1

I have talked about a symbol having a monad and dyad interpretation. Here is one example. Used as a dyad ^ means raising to a power, as in:

3 ^ 2

But used as a monad, it means $e^x$:

^ 2

Next, let us take a look at some functional operators. We shall use the trigonometric functions, which we load as

load'trig'

Then we can create

f=: sin + cos
g=: ^ * sin
h=: sin @ cos
i=: ^ @ cos

Here $f(x) = \sin x+\cos x$, $g(x) = e^x\sin x$, $h(x) = \sin(\cos x)$ and $i(x)=e^{\cos x}.$ The first two are examples of forks.

Next let us see insertion in action. Suppose we want to compute $$ 1 + 3 + 4 + 5 + 10. $$ This means inserting the dyad + between each successive pair. So we can write

+ / 1 3 4 5 10

Guess the outcome of

- / 1 1 1 1 1

Most often the / operator is used to accumulate some result recursively (e.g., summing). You can use this to find minimum or maximum as well, .e.g,

<./ 1 4 3 8 4

Another important class of operators take slices of dyads to produce monads. The slice could be along the $y$-axis (i.e., fixing some value of $x$) like $y\mapsto f(a,y).$ Or it could be aong the $x$-axis, like $x\mapsto f(x,b).$ Or t could be along the diagonal $t\mapsto f(t,t).$ These are, respectively, a & f, f & b and f~.

Table of contents

Learning J

First taste of J