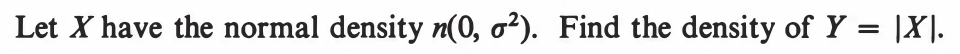
EXERCISE 1: [hpspdf28.png]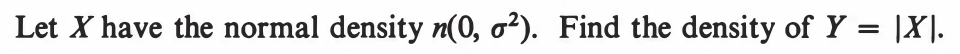
EXERCISE 2: [rossdistrib12.png]
EXERCISE 3: Find $V(X)$ if $X\sim Beta(a,b)$ for $a,b>0.$
EXERCISE 4: Let $(X,Y)$ be a random point in ${\mathbb R}^2$, where $X,Y$ are IID $N(0,1).$ Let $(R,\Theta)$ be the same point in polar coordinates. Find the joint distribution of $(R,\Theta).$
EXERCISE 5: If $X\sim Cauchy,$ then show that $\frac 1X\sim Cauchy$, as well.
EXERCISE 6: If $X\sim N(\mu,\sigma^2)$, then $Y=e^X$ is said to have log-normal$(\mu,\sigma^2)$ distribution. Show that $E(Y^k)$ exists finitely for all $k\in{\mathbb N}.$ Also show that MGF $m(t)$ of $Y$ does not exist anywhere except for $t\leq 0.$
EXERCISE 7: Let $\left[\begin{array}{ccccccccccc}X_1\\X_2 \end{array}\right]\sim N_2\left( \left[\begin{array}{ccccccccccc}\mu_1\\\mu_2 \end{array}\right],\left[\begin{array}{ccccccccccc}\sigma^2_1 & \rho \sigma_1 \sigma_2\\ \rho \sigma_1 \sigma_2 & \sigma^2_2 \end{array}\right]\right)$, where $\rho\in(-1,1)$ and $\sigma^2_1,\sigma^2_2 > 0.$ Let $a\in{\mathbb R}$ be any number. Show that given $X_1=a$ the conditional distribution of $X_2$ is $$N\left(\mu_2+\frac{\rho \sigma_2}{\sigma_1}(a-\mu_1), (1-\rho^2)\sigma^2_2\right).$$ Show this by direct computation (not as a corollary to some other exercise from the class webpage).
EXERCISE 8: Let $\v \Pi$ be a random vector $(\Pi_1,...,\Pi_k)$ having distribution $\v \Pi\sim Dir(a_1,...,a_{k+1}).$ Let the conditional distribution of $\v X$ given $\v\Pi$ be $Multinom(n,(\Pi_1,...,\Pi_k,1-\Pi_1-\cdots\Pi_k),).$ Then show that the conditional distribution of $\v \Pi$ given $\v X$ is $Dir(a_1+X_1,...,a_{k+1}+X_{k+1}).$
EXERCISE 9: If $X_1,X_2$ are independent $Gamma(a_1,p)$ and $Gamma(a_2,p)$ random variables, then show that $$\frac{X_1}{X_1+X_2}\sim Beta(a_1,a_2).$$
EXERCISE 10: Let $\v X\sim N_n(\v 0, I)$ and $J_{n\times n}$ have all entries equal to 1. Find the distribution of $\v X' J\v X.$