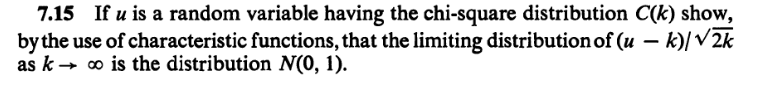[Home]

Multivariate normal and related distributions

$\newcommand{\v}[1]{\boldsymbol{#1}}$ $\newcommand{\k}[1]{\chi^2_{(#1)}}$ Multivariate normal and related distributions

Multivariate normal distribution (part 1)

Video for this section

Here we shall discuss the most commonly used multivariate distribution, the multivariate normal distribution.

First we shall recast the defnition of univariate normal from the last chapter to a form suitable for generalisation to higher dimensions. Instead of defining $N(\mu,\sigma^2)$ via density, we shall start with just $N(0,1)$ and define it via the density $\frac{1}{\sqrt{2\pi}} e^{-x^2/2},~~x\in{\mathbb R}.$ Then for any $\sigma^2 \geq 0$ we can define $N(\mu,\sigma^2)$ as the distribution of $\sigma X+\mu,$ whre $X\sim N(0,1).$ Convince yourself that this is equivalent to what the definition of univariate normal given in the last chapter, and that this includes the $\sigma^2=0$ case also.

Now we are ready for the multivariate generalisation. For $N(\mu, \sigma^2)$ the parameters were $\mu\in{\mathbb R}$ and $\sigma^2\geq 0.$ In $m$-dim our parameters will be a vector $\v\mu\in{\mathbb R}^m$ and a NND matrix $\Sigma_{m\times m}. $ We shall need the following fact about NND matrices from linear algebra:
Theorem A matrix $\Sigma_{m\times m}$ is NND if and only if $\Sigma = AA'$ for some $A_{m\times n}$ for some $n\in{\mathbb N}.$

Proof:Should be covered in your Vectors and Matrices course.[QED]

At last we come to the definition of multivariate normal.
Definition: Multivariate normal For any $\v\mu\in{\mathbb R}^m$ and any NND $\Sigma_{m\times m}$ we define $N_m(\v\mu, \Sigma)$, the $m$-dimensional multivariate normal distribution as the distribution of $\v Y=A\v X + \v \mu$, where $\v X_{m\times 1}$ has IID $N(0,1)$ components, and $A_{m\times m}$ is any matrix such that $\Sigma = AA'.$
The only point that you might feel uncomfortable about is the choice of $A.$ In the univariate case, obtaining $\sigma$ from $\sigma^2$ was straightforward: we could just take the (unique) nonnegative square root. But in the multivariate set up there are, in general, infinitely many choices for $A$ such that $\Sigma=AA'.$ Which one should we take? Fortunately it does not matter here, because as we are going to show now, any choice leads to the same distribution of $A\v X+\v\mu.$

For this purpose we shall use characteristic functions.

Problem set 1

EXERCISE 1: Follow the definition to obtain the density of $\v Y = \left[\begin{array}{ccccccccccc}Y_1\\Y_2 \end{array}\right]\sim N_2\left(\left[\begin{array}{ccccccccccc}10\\20 \end{array}\right],\left[\begin{array}{ccccccccccc}1 & 0\\0 & 4 \end{array}\right]\right).$ You may use $A = \left[\begin{array}{ccccccccccc}1 & 0\\0 & 2 \end{array}\right].$

Multivariate normal distribution (part 2)

Video for this section

Justifying the defintion using characteristic function

In the multivariate set up, characteristic function is defined as follows.

Definition: Multivariate characteristic function Let $\v U = (U_1,...,U_m)'$ be a random vector. Then its characteristic function is defined as $\xi:{\mathbb R}^m\rightarrow{\mathbb C}$ where $$\xi(t_1,...,t_m)\equiv \xi(\v t) = E(e^{i\v t'\v U}).$$
The following theorem, which is an obvious analogue for the corresponding univariate theorem, is what makes characteristic function useful.
Theorem For any ${\mathbb R}^m$-valued random vector, its characteristic function exists. Also, the characteristic function uniquely determines the distribution.

Proof:Not in this course.[QED]

Now let us return to the definition multivariate normal.

Back to normal

We shall take any $A$ with $\Sigma=AA',$ and show that the characteristic function of $\Sigma\v X+\v\mu$ will depend on $A$ only through $AA'=\Sigma.$ So the particular choice of $A$ will not matter.

We shall start with the characteristic function of $\v X$: $$E(\exp(i\v t'\v X) = E(e^{it_1X_1+\cdots it_nX_n}) =E(e^{it_1X_1}\cdots e^{it_nX_n})= E(e^{it_1X_1})\cdots E(e^{it_nX_n})) = e^{-t_1^2/2}\cdots e^{-t_n^2/2} = \exp\left(-\frac 12\v t'\v t\right).$$ So the characteristic function of $A\v X + \v \mu$ is $$\begin{eqnarray*} E(\exp(i\v t'(A\v X+\v \mu)) & = & E(\exp(i((A'\v t)'\v X+\v t'\v \mu))\\ & = & \exp\left(-\frac 12\v t'AA'\v t+i\v t'\v\mu\right)\\ & = & \exp\left(-\frac 12\v t'\Sigma\v t+i\v t'\v \mu\right), \end{eqnarray*}$$ which indeed does not involve $A.$

As a by product of the above steps we also get the characteristic function of $N_m(\v\mu,\Sigma).$

Problem set 2

EXERCISE 2: Write down the characteristic function of $N_2(\v\mu,\Sigma)$ where $\v\mu=\left[\begin{array}{ccccccccccc}1\\2 \end{array}\right]$ and $\Sigma=\left[\begin{array}{ccccccccccc}2&1\\1&3 \end{array}\right].$

EXERCISE 3: There are algorithms that will take $\Sigma$ as input and produce an $A$ as output suh that $\Sigma=AA'.$ The Cholsesky (read as ko-less-key) decomposition algorithm is one such (implemeted in the R function chol). But for small matrices, it is possible to construct $A$ by hand. Suppose $\Sigma=\left[\begin{array}{ccccccccccc}2&1\\1&3 \end{array}\right].$ Find a lower triangular $A$ with $\Sigma=AA'.$

EXERCISE 4: Find $$\v\mu$ $ and $\Sigma$ if $N_2(\v\mu,\Sigma)$ has characteristic function $\xi(t_1,t_2) = \exp(-2t_1^2-t_2^2+t_1t_2)$ for $(t_1,t_2)\in{\mathbb R}^2.$

EXERCISE 5: True or false: The characteristic function of $N_m(\v\mu,\Sigma)$ is real-valued if and only if $\v\mu=\v0.$

Multivariate normal distribution (part 3)

Video for this section

Theorem If $\v Y\sim N_m(\v \mu, \Sigma)$ and $B_{n\times m}$ and $\v c_{n\times 1}$ are fixed, then $\v Z = B\v Y+\v c\sim N_n(B\v \mu + \v c, B\Sigma B').$

Proof: Be careful that the variance matrix is $B\Sigma B'$ and not $B'\Sigma B.$

Let $\Sigma = AA'.$ Then, by definition, $\v Y$ has the same distribution as that of $A\v X+\v\mu,$ where $\v X\sim N_m(\v,I).$

So $B\v Y+\v c$ has the same distribution as that of $B(A\v X+\v\mu)+\v c = BA\v X + (B\v\mu+\v c).$ This is, by definition, $N_n(B\v\mu+\v c, BAA'B') = N_n(B\v\mu+\v c, B \Sigma B').$ [QED]

The theorem could also be proved using characteristic function.

Two corollaries

Here is the first corollary.
Theorem If $\v X = (X_1,...,X_n)'\sim N_n(\v \mu,\Sigma),$ then any subvector of $\v X$ has multivariate normal distribution with the corresponding subsector of $\v \mu$ and corresponding principal submatrix of $\Sigma.$

Proof: Extracting a subvector is same as premultiplying by a matrix. The matrix is obtained by selecting appropriate rows of the identity matrix.

Apply the affine transform result with $B=$ this matrix and $\v c=\v0$ to prove this theorem. [QED]

The second corollary is the multivariate analogue of univariate standardisation: If $X\sim N(\mu,\sigma^2)$ for $\sigma^2>0,$ then $\frac{X-\mu}{\sigma}\sim N(0,1).$

Theorem Let $\v X\sim N_n(\v\mu,\Sigma)$ where $\Sigma$ is nonsingular. Let $\Sigma = AA'$ for $A_{n\times n}.$ Then $A ^{-1} (\v X-\v\mu)\sim N_n(\v0,I).$

Proof: Direct application of the theorem. Just notice that $A$ must be nonsingular, because had it been singular, $AA'$ would have been singular, as well. [QED]

Problem set 3

EXERCISE 6: Let $$\left[\begin{array}{ccccccccccc}X_1\\X_2\\X_3\\X_5\\X_5 \end{array}\right]\sim N_5\left(\left[\begin{array}{ccccccccccc}1\\2\\3\\4\\5 \end{array}\right],\left[\begin{array}{ccccccccccc}50 & 42 & 41 & 48 & 27\\ 42 & 40 & 38 & 40 & 25\\ 41 & 38 & 51 & 53 & 39\\ 48 & 40 & 53 & 61 & 39\\ 27 & 25 & 39 & 39 & 38 \end{array}\right]\right). $$ Find the distribution of $\v Y = (2X_1-3X_4+X_5,~~X_1+X_4)'.$

[Hint: Don't struggle with the full $5\times5$ matrix.]

EXERCISE 7:  If $X_1,...,X_n$ are IID $N(0,1).$ Let $\v X = (X_1,...,X_n)'.$ Let $A_{n\times n}$ be any orthogonal matrix. Then show that the components of $A\v X$ are again IID $N(0,1).$

[Hint]

Here $\v X\sim N_n(\v0,I).$ So $A\v X\sim N_n(A\v0,AIA') = N_n(\v0,I),$ since $A$ is orthogonal.

Multivariate normal distribution (part 4)

Video for this section

Mean and dispersion

It is easy to find the mean vector and variance matrix of a multivariate normal distribution:
Theorem If $\v Y\sim N_m(\v\mu,\Sigma)$, then $E(\v Y)=\v \mu$ and $V(\v Y) = \Sigma.$

Proof: Let $\Sigma = AA'.$ Then $\v Y$ has the same distribution as $A\v X+\v \mu$ where the $\v X$ has components IID $N(0,1).$

So $E(\v X) = \v 0$ and $V(\v X) = I.$

Hence $E(\v Y) = E(A\v X+\v\mu) = A E(\v X)+\v\mu = \v\mu,$ and $V(\v Y) = V(A\v X+\v\mu) = A V(\v X)A' = AA'=\Sigma.$ [QED]

Problem set 4

EXERCISE 8: Find $E(\v X)$ and $V(\v X)$ if $\v X$ has characteristic function $\xi(t_1,t_2) = \exp(-2t_1^2-t_2^2+t_1t_2)$ for $(t_1,t_2)\in{\mathbb R}^2.$

EXERCISE 9: If $\v X\sim N_m(\v\mu,\Sigma)$ and the components of $\v X$ are all independent, then what can you say about the structure of $\Sigma?$

Multivariate normal distribution (part 5)

Video for this section

Independent vs zero covariance

If two random variables are independent, they must also have covariance zero. However, the converse is not true in general. For multivariate normal the converse is also true. For this we need the following result about characteristic function:

Theorem If $\v X$ and $\v Y$ are two random vectors with characteristic functions $\xi_X(\v s)$ and $\xi_Y(\v t)$, then the characteristic function of $\v Z = \left[\begin{array}{ccccccccccc}\v X\\\v Y \end{array}\right]$ is $\xi_Z(\v s,\v t)=\xi_X(\v s)\xi_Y(\v t)$ if and only if $\v X$ and $\v Y $ are independent.

Proof:Direct application of definition.[QED]

TheoremIf $$\v X = \left[\begin{array}{ccccccccccc}\v X_1\\\v X_2 \end{array}\right]'\sim N_n\left(\underbrace{\left[\begin{array}{ccccccccccc}\v \mu_1\\\v \mu_2 \end{array}\right] }_{\v\mu}, \underbrace{\left[\begin{array}{ccccccccccc}\Sigma_{11} & \Sigma_{12}\\\Sigma_{12}' & \Sigma_{22} \end{array}\right] }_\Sigma\right),$$ then $\v X_1$ and $\v X_2$ are independent if and only if $\Sigma_{12} = O.$

Proof: The characteristic function of $\v X$ is $\xi_{\v X}(\v t)=\exp\left(-\frac 12\v t'\Sigma\v t+i\v t'\v \mu\right).$

Writing $\v t =\left[\begin{array}{ccccccccccc}\v t_1\\\v t_2 \end{array}\right], $ we have $$\v t'\Sigma\v t =\left[\begin{array}{ccccccccccc}\v t_1' & \v t_2' \end{array}\right]\left[\begin{array}{ccccccccccc}\Sigma_{11} & \Sigma_{12}\\\Sigma_{12}' & \Sigma_{22} \end{array}\right]\left[\begin{array}{ccccccccccc}\v t_1\\\v t_2 \end{array}\right] = \v t_1'\Sigma_{11}\v t_1+ \v t_1'\Sigma_{22}\v t_2,$$ since $\Sigma_{12}=O.$

Again $$\v t'\v \mu = \left[\begin{array}{ccccccccccc}\v t_1' & \v t_2' \end{array}\right]\left[\begin{array}{ccccccccccc}\v \mu_1 & \v \mu_2 \end{array}\right] = \v t_1'\v \mu_1+\v t_2'\v \mu_2$$ So the characteristic function factorises as $$\xi_{\v X}(\v t)\equiv \xi_{\v X_1}(\v t_1)\xi_{\v X_1}(\v t_2),$$ and hence $\v X_1$ and $\v X_2$ are independent, as required. [QED]

An important corollary is the following result.

TheoremIf $\v X\sim N_n(\v\mu, I)$ and $A_{p\times n}$ qr $B_{q\times n}$ are any two fixed matrices with $AB'=O,$ then $A\v X$ and $B\v X$ must be independent.

Proof: Immediate rom the theorem (try it!). [QED]

A further corollary is
TheoremSuppose that $\v X\sim N_n(\v\mu, I)$ and let $S, T$ be two mutually orthogonal subspaces of ${\mathbb R}^n.$ Let $\v Y$ and $\v Z$ be orthogonal projections of $\v X$ on $S$ and $T,$ respectively. Then $\v Y$ and $\v Z$ must be independent.

Proof:

Let $P_S$ and $P_T$ be the orthogonal projection operators for $S$ and $T.$ Then they are both symmetric idempotent matrices with $P_SP_T = 0.$

Now apply the last theorem. [QED]

Problem set 5

EXERCISE 10: Let $\v X\sim N_n(\v\mu,I).$ Let $\v a, \v b\in{\mathbb R}^n$ be orthogonal to each other. Show that $\v a'\v X$ and $\v b'\v X$ must be independent.

EXERCISE 11: Let $\left[\begin{array}{ccccccccccc}\v X_{m\times 1}\\\v Y \end{array}\right] \sim N_{m+n}\left(\left[\begin{array}{ccccccccccc}\v \mu_1\\\v\mu_2 \end{array}\right], \left[\begin{array}{ccccccccccc}A_{m\times m} & B\\B' & C \end{array}\right]\right).$ What is the distribution of $\v X$ and $\v Y$ separately?

EXERCISE 12: (Continuation of the last problem) If $A$ is nonsingular, then show that $\v Y-B'A ^{-1}\v X$ and $\v X$ are independent.

EXERCISE 13: (Continuation of the last problem) Write $\v Y = B'A ^{-1} \v X + (\v Y-B'A ^{-1}\v X)$ and show that the conditional distribution of $\v Y$ given $\v X=\v x$ is $N_n (\v \mu_2+B'A ^{-1}(\v x-\v\mu_1), C-B'A ^{-1} B).$ [Does this remind you of multiple regression?]

[Hint]

Let us write the condl distribution as $Distr(\v Y|\v X=\v x)$.

Then $$\begin{eqnarray*} Distr(\v Y|\v X=\v x) & = & Distr(B'A ^{-1} \v X + (\v Y-B'A ^{-1}\v X)|\v X=\v x)\\ & = & Distr(B'A ^{-1} \v x + (\v Y-B'A ^{-1}\v X)|\v X=\v x)\\ & = & B'A ^{-1} \v x +Distr( \v Y-B'A ^{-1}\v X|\v X=\v x)\\ & = & B'A ^{-1} \v x +Distr( \v Y-B'A ^{-1}\v X)~~\left[\mbox{$\because$ indep}\right] \end{eqnarray*}$$ Now $$\v Y-B'A ^{-1}\v X = \left[\begin{array}{ccccccccccc}-B A ^{-1} & I \end{array}\right]\left[\begin{array}{ccccccccccc}\v X\\\v Y \end{array}\right].$$ So $Distr( \v Y-B'A ^{-1}\v X)$ may be computed easily.

EXERCISE 14: Let $\v X\sim N_n(\v0,I).$ We take some subspace of ${\mathbb R}^n,$ and project $\v X$ on it to get a vector $\v Y.$ Let $\v Z = \v X-\v Y.$ The situation is depicted pictorially below.

Show that $\v Y$ and $\v Z$ are independent.

Multivariate normal distribution (part 6)

Video for this section

As we have already mentioned, a multivariate normal distribution need not always have a density. However, for an important special case, it does. This case is called the nonsingular case, while the other case is called singular. The case is determined by the $\Sigma$ matrix. If it is nonsingular, then we have density, else not. We prove these next.

Nonsingular: When density exists

TheoremIf $\Sigma$ is a nonsingular matrix, then $N_m(\v\mu,\Sigma)$ has density $$\frac{1}{\sqrt{(2\pi)^n det(\Sigma)}}\exp\left(-\frac 12(\v y-\v\mu)'\Sigma ^{-1}(\v y-\v\mu)\right)\mbox{ for }\v y\in{\mathbb R}^n,$$

Proof: Since $\Sigma$ is NND, we can write $\Sigma = AA'$ for some $A_{m\times m}.$ So $N_m(\v\mu,\Sigma)$ is the distribution of $A\v X+\v\mu,$ where $\v X$ has IID $N(0,1)$ components.

Clearly, the density of $\v X$ is $$\frac{1}{\sqrt{(2\pi)^n}}\exp\left(-\frac 12\v x'\v x\right)\mbox{ for }\v x\in{\mathbb R}^n.$$ Now, since $\Sigma$ is nonsingular, so must be $A$, and hence the transform $\v Y = A\v X+\v \mu$ is a bijection.

The inverse transform is $\v X = A ^{-1}(\v Y-\v\mu).$

The Jacobian of this inverse transform is $A ^{-1}.$

So the Jacobian formula gives (check!) the following density for $\v Y = A\v X+\v \mu$ $$\frac{|det(A ^{-1})|}{\sqrt{(2\pi)^n}}\exp\left(-\frac 12(\v y-\v\mu)'(A ^{-1})'A ^{-1}(\v y-\v\mu)\right)\mbox{ for }\v y\in{\mathbb R}^n.$$ Since $\Sigma = AA',$ hence $|det(A ^{-1})| = \frac{1}{\sqrt{det(\Sigma)}}$ and $(A ^{-1})'A ^{-1} = (AA') ^{-1} = \Sigma ^{-1}.$

So the density may be written as $$\frac{1}{\sqrt{(2\pi)^n det(\Sigma)}}\exp\left(-\frac 12(\v y-\v\mu)'\Sigma ^{-1}(\v y-\v\mu)\right)\mbox{ for }\v y\in{\mathbb R}^n,$$ as required. [QED]

Singular: when density does not exist

The other half does not even need any normality assumption.

TheoremIf $V(\v Y)$ is a singular matrix, then $\v Y$ cannot have a density.

Proof: Let $\v Y$ have dispersion matrix $\Sigma$ which is singular.

Let, if possible, $\v Y$ have density.

Then $\exists \v a\neq\v0~~\Sigma \v a = \v 0.$ So $\v a'\Sigma \v a = 0.$

But $\v a'\Sigma \v a = V(\v a' \v Y),$ hence we see that $\v a'\v Y$ must be a constant with probability 1.

We can extend $\{\v a\}$ to a basis $\{\v a,...\}$ of ${\mathbb R}^m.$

Let $P = \left[\begin{array}{ccccccccccc}\v a & \cdots \end{array}\right]$ be the matrix with these as columns.

Then $P$ is nonsingular, and so $\v Z = P'\v Y$ is a bijective transform of $\v Y.$

So, by the Jacobian formula, $\v Z$ must also have joint density. Then its first component $\v a'\v Y$ must also have a (marginal) density. But that is impossible, since it is a degenerate random variable.

Hence the result. [QED]

Problem set 6

EXERCISE 15: Describe $N_2(\v0,I)$ distribution.

EXERCISE 16: Let $$\left[\begin{array}{ccccccccccc}X\\Y \end{array}\right] \sim N_2\left(\left[\begin{array}{ccccccccccc}1\\2 \end{array}\right], \left[\begin{array}{ccccccccccc}1 & -1\\-1 & 1 \end{array}\right]\right).$$ If we take data $(x_1,y_1),...,(x_n,y_n)$ from $(X,Y)$, what will the scatterplot look like?

$\chi^2$ distribution

Video for this section

Starting from this section, we shall discuss some distributions related to the normal distribution.
Definition: $\chi^2$If $X_1,...,X_n$ are IID $N(0,1)$ then the distribution of $\sum_1^n X_i^2$ is called chi-square distribution with degrees of freedom $n.$ We write $$\sum_1^n X_i^2\sim \chi_{(n)}^2.$$
Theorem $\k n$ is the same as $Gamma\left(\frac 12,\frac n2\right).$

Proof: Let $X_1,...,X_n$ be IID $N(0,1).$

Then $X_1^2$ has CDF $F(\cdot),$ where $F(a)=0$ for $a<0$ and for $a\geq 0$ we have $$F(a) = P(X_1^2\leq a) =\frac{1}{\sqrt{2\pi}} \int_{-\sqrt a}^{\sqrt a} e^{-x^2/2}\, dx=\frac{2}{\sqrt{2\pi}} \int_0^{\sqrt a} e^{-x^2/2}\, dx.$$ Differentiating wrt $a$ we get the density $$f(a) = F'(a) = \frac{2}{\sqrt{2\pi}} e^{-a/2}\mbox{ for }a>0.$$ We immediately recognise it as the $Gamma\left(\frac 12,\frac 12\right)$ density.

So $X_i^2\sim Gamma\left(\frac 12,\frac 12\right)$ for $i=1,2,...,n.$

Also they are independent.

So, by the additivity property of the $Gamma$ distribution, we have $\sum_1^n X_i^2 \sim Gamma\left(\frac{1}{2},\frac n2\right).$

Hence $\k n\equiv Gamma\left(\frac{1}{2},\frac n2\right),$ as required. [QED]

Since we have already learned that the characteristic function of $Gamma(p,\alpha)$ is $\left(\frac{p}{p-it}\right)^\alpha,$ hence we have the following characteristic function for the $\k n$ distribution:

Characteristic function of $\chi^2_{(n)}$ The characteristic function of $\k n$ is $\xi(t) = (1-2it)^{-n/2}$ for $t\in{\mathbb R}.$

Proof: Put $p=\frac 12$ and $\alpha=\frac n2$ in the characteristic function of $Gamma(p,\alpha).$ [QED]

Geometry of $\chi^2_{(k)}$

Video for this section

If we consider a random vetor $\v X$ in ${\mathbb R}^k$ with IID $N(0,1)$ components, $\|\v X\|^2\sim \k k.$ This is little more than the definition.

TheoremNow let be $\v X\sim N_n(\v 0, I).$ Let $S$ be any $k$-dimensional subspace of ${\mathbb R}^n. $ Consider the orthogonal projection $\v Y$ of $\v X$ onto $S.$ Then $$\|\v Y\|^2\sim \k k.$$

Proof: We take any ONB of $S$ and extend it to an ONB of ${\mathbb R}^n. $ Pack the ONB as rows to get an orthogonal matrix $Q.$

Then $\v Z=Q\v X\sim N_n(\v 0, I).$

Also $\|\v Y\|^2 = \sum_1^k Z_i^2\sim\k k,$ as required. [QED]

Definition: Non-central $\chi^2$ If $X_1,...,X_n$ are independent $N(\mu_i,1),$ then the distribution $\sum X_i^2$ is called noncentral $\k n$ with noncentralty parameter $\sum_i\mu_i^2.$

Problem set 7

EXERCISE 17: Let $\v X\sim N_n(\v \mu, I).$ Let $S$ be any $k$-dimensional subspace containing $\v \mu.$ Then show that the orthogonal projection of $\v X$ onto $S^\perp$ must have $\k {n-k}$ distribution.

EXERCISE 18: (Continuation of the last problem) How will the answer to the last problem change if $\v\mu\not\in S?$

Sampling distributions for normal sample

Video for this section

Theorem Let $X_1,...,X_n$ be a random sample (i.e., IID) from $N(\mu, \sigma^2).$ We consider the sampe mean $\bar X=\frac 1n\sum _1^nX_i$ and sample variance $S^2=\frac 1n\sum_1^n (X_i-\bar X)^2.$ Then
  1. $\bar X\sim N\left(\mu,\frac{\sigma^2}{n}\right)$
  2. $\frac{nS^2}{\sigma^2}\sim \k {n-1}$
  3. $\bar X$ and $S^2$ are independent.

Proof:Without loss of generality, we take $\mu=0$ and $\sigma=1.$

[Because...]
Once we have proved the $\mu=0$ case, we can work with $\mu+\sigma X_i$ to get the general form.
In ${\mathbb R}^n$ consider the subspace $V=span\{\v 1\},$ where $\v 1$ is the vector of al $1$'s. Clearly, $dim(V)=1$ and $dim(V^\perp)=n-1.$

We have learnt that in ${\mathbb R}^n$ the component (i.e., orthogonal projection) of one vector $\v v$ along another vector $\v u$ is $\frac{\v u'\v v}{\v u'\v u}\v u.$

So the orthogonal projection of $\v X$ along $\v 1$ (i.e., on $V$) is $\bar X\v 1.$

Hence the orthogonal projection of $\v X$ on $V^\perp$ is $$\v Y = \v X-\bar X\v 1 = \left[\begin{array}{ccccccccccc}X_1-\bar X\\\vdots\\X_n-\bar X \end{array}\right].$$ So from earlier result, we immediately see that these two projections must be independent.

Now $\bar X$ is a function of the first projection, while $S^2$ is a function of the second. So they are independent.

Also $nS^2 = \|\v Y\|^2\sim \k{n-1}.$

The distribution of $\bar X$ is obvious from an earlier theorem. [QED]

Problem set 8

EXERCISE 19:  Same set up as in the theorem above. What will the distribution of $\sum_1^n (X_i-a)^2$ be, where $a\in{\mathbb R}$ is a fixed number?

$t$ distribution

Video for this section

Definition: $t$-distribution If $X\sim N(0,1)$ and $Y\sim\k n$ and they are independent, then the distribution of $X/(\sqrt{Y/n})$ is called $t$-distribution with $n$ degrees of freedom. Here $n>0$ need not be an integer.
Let us derive density of $t$-distribution with $n$ degrees of freedom. We shall do this step by step.

From $Y$ we shall pass on to $Z = \sqrt{\frac Yn}$ and then to $\frac XZ.$

Y has density $f_Y(y) =\left\{\begin{array}{ll}\mbox{const } e^{-\frac y2}y^{\frac n2-1}&\text{if }y>0\\ 0&\text{otherwise.}\end{array}\right. $

The transform to go from $Y$ to $Z$ is $z = h(y) = \sqrt{\frac yn}$ with inverse $y = h ^{-1}(z) = n z^2.$

Hence, by the Jacobian formula, $Z$ has density $$f_Z(z) = 2nz f_Y(nz^2) = \left\{\begin{array}{ll}\mbox{const } e^{-nz^2/2} z^{n-2}&\text{if }z>0\\ 0&\text{otherwise.}\end{array}\right.$$ Next we shall employ the quotient formula to find density of $T = \frac XZ$ as $$\begin{eqnarray*} f_T(t) & = & \int_0^\infty u f_X(tu) f_Z(u)\, du\\ & = & \mbox{const} \int_0^\infty u e^{-t^2u^2/2} e^{-nu^2/2} u^{n-2}\, du\\ & = & \mbox{const} \int_0^\infty u^{n-1} e^{-(t^2+n)u^2/2}\, du. \end{eqnarray*}$$ Substituting $v = \frac{u^2}{2}$ we have $$\begin{eqnarray*} & = & \mbox{const} \int_0^\infty v^{\frac{n-1}{2}} e^{-(t^2+n)v}\, dv\\ & = & \mbox{const} \int_0^\infty v^{\frac{n+1}{2}-1} e^{-(t^2+n)v}\, dv\\ & = & \mbox{const } \Gamma\left(\frac{n+1}{2}\right) (t^2+n)^{-\frac{n+1}{2}} & = & \mbox{const } (t^2+n)^{-\frac{n+1}{2}}. \end{eqnarray*}$$ If you keep track of the constants, you will find that it is $$\frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\times n^{\frac{n+1}{2}}.$$ It should not be difficult to see that $t$-density is symmetric around 0. The densities are much like the $N(0,1)$ density. They lie somewhere in-between the Cauchy density and $N(0,1)$ density. As the degrees of freedom increase to $\infty,$ the $t$-distribution approaches $N(0,1).$ For degrees of freedom more than 40, the $t$-density is virtually indisguishable from that of $N(0,1)$ density.

Problem set 9

EXERCISE 20: Let $X_1,...,X_n$ be a random sample from $N(\mu,\sigma^2).$ Then what is the distribution of $$\frac{\sqrt n(\bar X-\mu)}{\sqrt{\sum(X_i-\bar X)^2/(n-1)}}?$$

$F$ distribution

Video for this section

Definition: $F$-distribution If $X\sim \k m$ and $Y\sim \k n$ are independent random variables, then the distribution of $\frac{X/m}{Y/n}$ is called $F$ -distribution with numerator degrees of freedom $m$ and denominator degrees of freedom $n.$
The density of $X$ is $f_X(x) =\left\{\begin{array}{ll}\mbox{const }x^{\frac m2-1}e^{-\frac x2}&\text{if }x>0\\ 0&\text{otherwise.}\end{array}\right. $

Similarly, the density of $Y$ is $f_Y(x) =\left\{\begin{array}{ll}\mbox{const }y^{\frac n2-1}e^{-\frac y2}&\text{if }y>0\\ 0&\text{otherwise.}\end{array}\right. $

Hence density of $Z = \frac XY$ is $$\begin{eqnarray*} f_Z(z) & = & \int_0^\infty u f_X(zu)f_Y(u)\, du\\ & = & \mbox{const}\int_0^\infty u (zu)^{\frac m2-1}e^{-\frac{zu}{2}} u^{\frac n2-1}e^{-\frac u2}\, du\\ & = & \mbox{const }z^{\frac m2-1}\int_0^\infty u^{\frac{m+n}{2}-1}e^{-\frac{z+1}{2}u}\, du\\ & = & \mbox{const }z^{\frac m2-1}\Gamma\left(\frac{m+n}{2}\right) \left(\frac{z+1}{2}\right)^{-\frac{m+n}{2}}\\ & = & \mbox{const }z^{\frac m2-1}(z+1)^{-\frac{m+n}{2}}. \end{eqnarray*}$$ Hence the density of $\frac nmZ$ is $$f(x) =\left\{\begin{array}{ll}\mbox{const }x^{\frac m2-1}(mx+n)^{-\frac{m+n}{2}}&\text{if }x>0\\ 0&\text{otherwise.}\end{array}\right. $$

Problem set 10

EXERCISE 21: Let $X_1,...,X_m$ and $Y_1,...,Y_n$ be random samples from $N(\mu_1,\sigma^2)$ and $N(\mu_2,\sigma^2)$, respectively (same $\sigma^2).$ Then what is the distribution of $$\frac{\sum(X_i-\bar X)^2/(m-1)}{\sum(Y_i-\bar Y)^2/(n-1)}?$$

Distribution of quadratic forms (part 1)

Video for this section

Definition: Quadratic form By a quadratic form in $n$-variables we understand a function $q:{\mathbb R}^n\rightarrow{\mathbb R}$ of the form $$q(\v x) = \v x' A \v x$$ for some fixed real, symmetric matrix $A$.
Any quadratic form is a linear combination of terms like $x_i^2$ or $x_ix_j$ (for $i\neq j$). The definition implies that every real, symmetric matrix produces a quadratic form. Conversely, every quadratic form has a unique real, symmetric matrix associated with it.

EXAMPLE 1:  Write down the real, symmetric matrix associated with the quadratic form $q(x,y) = x_1x_2-x_2^2.$

SOLUTION: There are two variables, so the matrix will be a $2\times 2$ one. The diagonal entries will come from the coefficcients of the square terms: $\left[\begin{array}{ccccccccccc}0 & ?\\? & -1 \end{array}\right]$, and the off-diagonal entries will come from the cross product terms: $\left[\begin{array}{ccccccccccc}0 & \frac 12\\\frac 12 & -1 \end{array}\right].$ The rule is: $(i,j)$-th entry is half the coefficient of $x_ix_j.$ ■

In this section we shall deal with the following set up:
$X_1,...,X_n$ are IID $N(0,1),$ or, equivalently $\v X = (X_1,...,X_n)'\sim N_n(\v0,I).$ We have some real, symmetric matrix $A.$ We want to explore various necessary and sufficient condtions under which the quadratic form $\v X'A\v X$ will have a $\k k$ distribution, and how $k$ is related with $A.$

We had seen earlier that if $\v Y$ is the orthogonal projection of $\v X$ onto some subspace $T$ of ${\mathbb R}^n,$ then $\|\v Y\|^2\sim \k {dim(T)}.$ Since a matrix is an orthogonal projection matrix iff it is symmetric and idempotent, and the rank of he matrix equals the dimension of the space we project on, we get the following result.
Theorem Let $A$ be a symmetric, idempotent matrix. Then $\v X'A\v X\sim\k{rank(A)}.$
A sort of converse is also true, as shown in the next theorem.
Theorem Let $\v X\sim N_n(\v 0,I).$ Let $A$ be a real symmetric matrix. Then $\v X'A\v X\sim \k r$ for some $r\in{\mathbb N}.$ Then $A$ must be idempotent, and $r = rank(A).$

Proof: This proof requires spectral representation of real, symmetric matrices whch allows us to write $A$ as $A = P'DP$ for some orthogonal matrix $P$ and diagonal matrix $D.$

Then $\v X' A\v X = \v X'P' D P \v X = (P\v X)' D (P\v X).$

Now $\v Y=P\v X\sim N_n(\v0,I)$ and so we can write $(P\v X)' D (P\v X) = \sum_1^k d_i Y_i^2$, where $k=rank(A).$

The $Y_j$'s are IID $N(0,1)$ and so $Y_j^2$'s are IID $\k 1$ random variables with characteristic function $(1-2it)^{-1/2}.$

So the characteristic function of $\sum_1^k d_i Y_i^2$ is $$E\left[\exp\left(it\sum_1^k d_j Y_j^2\right)\right] = \prod_1^k E\left[\exp\left(it d_j Y_j^2\right)\right] = \prod_1^k \xi(t d_j) = \prod_1^k (1-2it d_j)^{-1/2}.$$ We want this to be the characteristic function of $\k r$ for some $r.$ So $$\prod_1^k (1-2it d_j)^{-1/2}=(1-2it)^{-r/2}.$$ In other words, we need $$(1-2it d_1)\cdots (1-2it d_k)=(1-2it)^r.$$ Matching degrees of both sides, we see $r=k.$

Also, matching coefficients of powers of $t,$ we see that $d_1=\cdots=d_k=1.$ Hence $A = P'\left[\begin{array}{ccccccccccc}I & O\\O & O \end{array}\right]P$. We know that any matrix of this form must be idempotent. This completes the proof. [QED]

Distribution of quadratic forms (part 2)

Video for this section

We know that sum of independent $\chi^2$ random variables is a again a $\chi^2$ random variable with degrees of freedom adding up. Here is a partial converse.
Theorem If $X\sim\k m$ and $Y$ is a nondegenerate independent random variable such that $X+Y\sim\k n$, then we must have $n> m$ and $Y\sim\k{n-m}.$

Proof: Let $Y$ have characteristic function $\xi(t).$ Then we have $(1-2it)^{-m/2} \xi(t) = (1-2it)^{-n/2}.$

Hence we must have $\xi(t) = (1-2it)^{-(n-m)/2}.$

Since $\xi(t)$ is the characteristic function of some nondegenerate random variable, hence $\xi(t)$ must be bounded and not identically equal to 1. So $n > m.$

Since characteristic function determines the distribution, hence $Y\sim\k{n-m},$ as required. [QED]

Fact from linear algebra If $A$ is idempotent, then $rank(A)=tr(A).$

Fisher-Cochran theorem Let $A_1,...,A_k$ be some $n\times n$ nonzero, real, symmetric matrices with $A_1+\cdots+A_k = I.$ Then the following are equivalent:
  1. $\forall i~~ A_i^2 =A_i.$
  2. $r(A_1)+\cdots+r(A_k) = n.$
  3. $\forall i\neq j~~ A_iA_j =O.$

Proof: (2) implies (1), (3): Let $A_i = B_iC_i$ be a rank factorisation. Then $$I = B_1C_1+\cdots+B_kC_k = \underbrace{\left[\begin{array}{ccccccccccc}B_1 & \cdots & B_k \end{array}\right] }_B\underbrace{\left[\begin{array}{ccccccccccc}C_1\\ \vdots \\ C_k \end{array}\right] }_C. $$ By (2) $B$ and $C$ are $n\times n.$ So they are inverse of each other.

Hence $CB = I,$ as well. In other words, $$\left[\begin{array}{ccccccccccc}C_1\\ \vdots \\ C_k \end{array}\right]\left[\begin{array}{ccccccccccc}B_1 & \cdots & B_k \end{array}\right]=I.$$ Hence $\forall i~~C_iB_i = I$ and $\forall i\neq j~~C_iB_j = O.$

So $A_i^2 = B_iC_iB_iC_i = B_iC_i= A_i.$

Also for $i\neq j$ we have $A_iA_j = B_iC_iB_jC_j = O.$

(3) implies (1): We have $A_1+\cdots+A_k=I.$ Multiplying both sides with $A_i$ we get $A_iA_1+\cdots+A_iA_k=A_i.$

Thanks to (3), only the $i$-th term survives in the LHS. So we have $A_i^2 = A_i,$ as required.

(1) implies (2): We have $tr(A_1)+\cdots+tr(A_k) = tr(I)=n.$

Since we have assumed (1), hence $tr(A_i)=r(A_i).$ So (2) follows. [QED]

Why do we care about the Fisher-Cochran theorem in probability or statistics? Because we often start with a random vector $\v X\sim N_n(0,I),$ and split $\|\v X\|^2$ into some quadratic forms $\|\v X\|^2 = \v X\v X = \v X'A_1\v X+\cdots+\v X'A_k\v X.$ Then the Fisher-Cochran theorem implies that if all the quadratic forms have $\chi^2$-distributions, then must also be independent, and their degrees of freedom must add up to $n.$

Miscellaneous problems

EXERCISE 22: If $X$ has a density of the form $f(x) \propto \exp(a+b+cx^2),~~x\in{\mathbb R},$ then find $E(X)$ and $V(X)$ in terms of $a,b,c.$ Also find median of $X.$

EXERCISE 23: Construct $(X,Y)$ such that marginally $X$ and $Y$ have $N(0,1)$ distribution, but $(X,Y)$ is not bivariate normal.

EXERCISE 24: Suppose that you have a software to generate IID replications from $N(0,1).$ Let $\mu\in{\mathbb R}^n$ and $\Sigma$ be any $n\times n$ PD matrix. Suggest how you can use the software to generate a single observation from $N_n(\mu,\Sigma).$ Assume that the software can perform matrix operations.

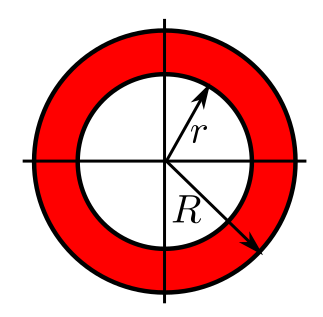
EXERCISE 25: If $X,Y$ are IID $N(0,1)$, then what is the chance that the random point $(X,Y)$ lies in the annulus shown below?

Express you answer in terms CDF of some standard distribution.

EXERCISE 26: Let $X_1,...,X_n$ be a random sample from $N(\mu,\sigma^2)$ for some $\mu\in{\mathbb R}$ and $\sigma^2>0.$ Find $a<b$ such that $P\left(a< \frac{\bar X-\mu}{S/\sqrt{n}} < b\right) = 0.95$ and $b-a$ is the least possible subject to this.

EXERCISE 27: [rossfcpnorm1.png]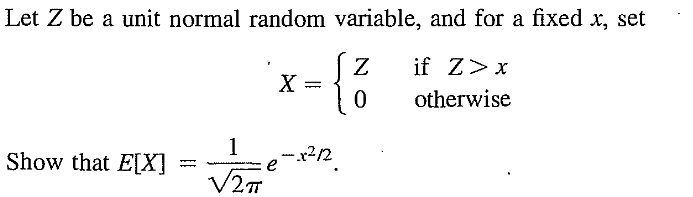

EXERCISE 28: [rossfcpnorm2.png]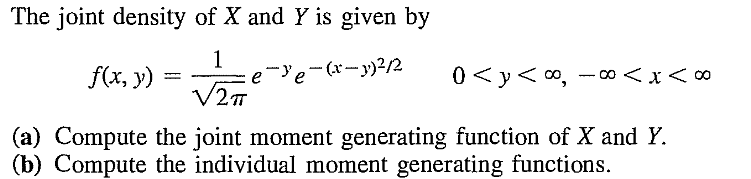

EXERCISE 29: [rossfcpnorm3.png]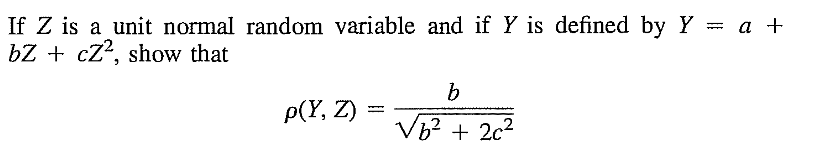

EXERCISE 30: [rossfcpnorm4.png]

EXERCISE 31: [rossfcpnorm5.png]

EXERCISE 32: [rossfcpnorm6.png]

EXERCISE 33: [rossfcpnorm7.png]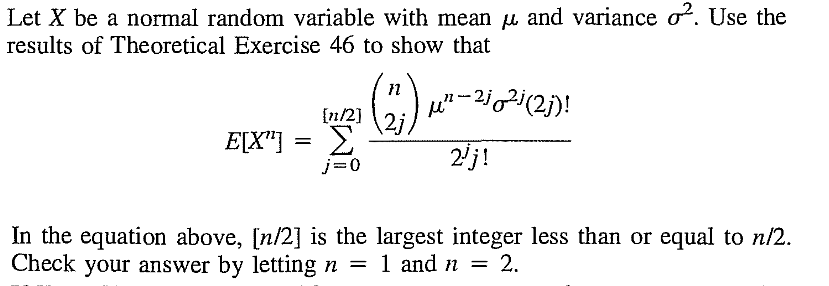

EXERCISE 34: [rossfcpnorm8.png]

EXERCISE 35: [rossipmnorm1.png]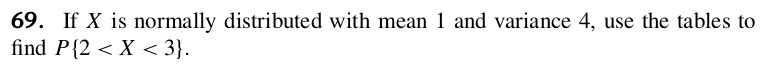

EXERCISE 36: [rossipmnorm2.png]

::

EXERCISE 37: [hpstrans19.png]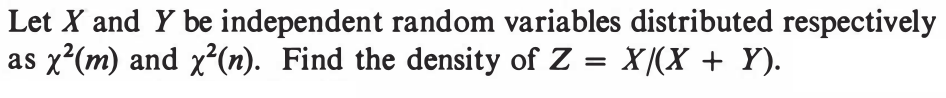

::

EXERCISE 38: [wilks9.png]